Explaining the Price Curve
If you have perused our data, you may have noticed the market average curve present on all our country graphs. This curve is so fundamental to MFTransparency that its characteristic downward slope is even represented in our logo. This is the curve relating interest rates to loan size, and it is extremely important in analyzing the price of microloan products. The recent New York Times article highlighted the high price that some MFIs charge in order to reap big financial gains from the poor. But it’s important to have a deeper understanding of this phenomenon: high prices don’t always mean big profits; the reason for high interest rates is more complex than this, as highlighted in this recent blog post from Elisabeth Rhyne at the Center for Financial Inclusion at ACCION International. The curve that MFTransparency uses to analyze loan rates is key in understanding pricing in microfinance. This blog post provides an overview of some of the informational materials that MFTransparency has come up with in order to help others understand pricing in microfinance.
The key factor in understanding the high price of microloans is operating expense. The fact is there are just some costs that all financial institutions face when disbursing a loan, regardless of the amount of that loan. For example they have to pay loan officers to manage the loans, organizational and computer systems to help with this process, etc. These costs don’t change predictably with loan size, and often they can actually be higher per loan for MFIs who must spend more time and energy to disburse loans in remote areas or to hard to reach populations.
In the end, if institutions want to be financially sustainable, they have to charge a price that covers all of their costs including this operating expense. To clarify with an example, let us assume that it costs $50 to disburse a loan. For a $100,000 loan this is a relatively negligible cost as a percentage of the loan, but for a $100 dollar loan it represents a significant percentage of the loan itself, and thus a much higher rate will need to be charged to cover this cost.
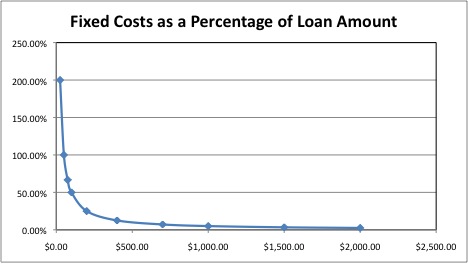
This relationship between interest rate and loan amount can also be represented graphically, and is the reason for the price curve that relates loan size to interest rate. The table and graph below demonstrate the relationship between loan size and price – specifically, a price that must cover a fixed cost of disbursing a loan. The table shows various loan sizes ranging from $25 to $50, and a fixed price of $50 for disbursing each. Of course, this situation is simplified, but it is meant to demonstrate that there are certain fixed costs associated with disbursing a loan that do not change with loan size. Finally, in the last row of the table we calculate the price (as a percentage of the overall loan amount) that an institution would have to charge in order to cover this fixed component of cost.
Fixed Cost as a Percentage of Loan Size
| Loan Size | $25.00 | $50.00 | $75.00 | $100.00 | $200.00 | $400.00 | $700.00 | $1,000.00 | $1,500.00 | $2,000.00 |
| Cost to Disburse | $50.00 | $50.00 | $50.00 | $50.00 | $50.00 | $50.00 | $50.00 | $50.00 | $50.00 | $50.00 |
| Cost/Loan Size | 200.00% | 100.00% | 66.67% | 50.00% | 25.00% | 12.50% | 7.14% | 5.00% | 3.33% | 2.50% |
When we graph this price versus loan amount we are presented with a power law relationship, that is to say the shape you see in the graph below. This is the mathematical relationship that we see when we divide a fixed cost by varying loan amounts. For this reason, MFTransparency uses power law curve when modeling loan price versus loan size. In reality, pricing is more complex than is implied by the simple scenario above. For example, an MFI may not want to vary interest rates for every different loan size offered. The MFI may therefore offer an entry-level product that doesn’t cover costs, knowing that the loss it incurs on this first loan will be made up by profits made on larger loans by the same client as she progresses through subsequent loan cycles. Or perhaps the MFI is able to streamline costs by cutting some services to clients with smaller loans. The important thing to bear in mind is that operating expense is a function of the number of loans disbursed for a given total loan portfolio, and not a function of total portfolio as an amount of money, and so the power-law relationship is still expected to be the underlying model constraining price. Put another way, this just means that it would be much cheaper for an institution to use a given portfolio amount to offer a few big loans rather than many small loans.
The overall result of this is that the cost of microloans is dominated by operating expense. At low average loan amounts, a fixed operating expense is large compared to the loan. Thus the ratio of operating cost to loan amount is high, and pricing decisions are dominated by this curved relationship between APR and loan amount. As loans get larger, a per loan fixed operating expense becomes increasingly negligible, and the curve becomes ever more shallow. The very fact that operating expense is fixed per loan differentiates microloans from macroloans; it is the most important determinant in price for small loans and a negligible factor for larger loans. As such, for those loans traditionally administered by banks, there is little focus on the effect of loan size on price. But this relationship is key when considering the price structure of microloans, where the slope is steep and the resulting price differential appreciable. The image below shows this graphically. Without getting too hung up on the specific loan amounts differentiating microloans from macroloans (which change from market to market), we can see how the power law curve that we derived above makes this price curve steep for microloans and very shallow for macroloans.
This is the reason why we can’t simply look at price and know whether the interest rate being charged is expensive or not. When considering other factors that affect the price of small loans, it is imperative to incorporate the effect of loan size as well. With larger loans it is often the case that the effect of loan amount can be largely discounted, and the focus can be put solely on other factors, such as the effect of the riskiness of the loan on loan price. Or of how profit margin relates to loan price. However, for for microloans, it is first necessary to control for loan size.





No Comments